Mengenal Balok

BALOK (CUBOID)

Balok adalah bangun tiga dimensi yang dibentuk oleh tiga pasang sisi yang berbentuk persegi atau persegi panjang dengan satu diantaranya berukuran berbeda

Ciri-ciri Balok :

• Balok memiliki 6 bidang sisi, dimana sisi yang sejajar sama besar
• Balok memiliki 12 rusuk, dimana rusuk yang sejajar sama panjang
• Balok memiliki 8 titik sudut yang semuanya siku-siku
• Balok memiliki 12 diagonal bidang, dimana diagonal bidang yang sejajar sama panjang
• Balok memiliki 4 diagonal ruang
• Balok memiliki 4 bidang diagonal

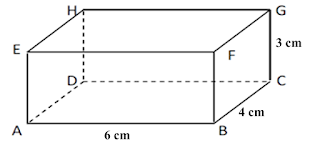
Ilustrasi :

Identifikasi :

• Sisi balok yang sama besar ; ABCD dan EFGH, ABFE dan CDHG, BCGF dan ADHE
• Rusuk balok ; 4 dengan panjang p, 4 dengan panjang l, 4 dengan panjang t
• Titik sudut ; A, B, C, D, E, F, G, dan H
• Diagonal bidang ; AC, BD, EG, FH, DE, AH, CF, BG, AF, BE, DG dan CH
• Diagonal ruang ; AG, BH, CE, dan DF
• Bidang diagonal ; ABGH, CDEF, ADGH, dan BCEH

Jaring-jaring Balok :
Jaring-jaring balok merupakan berbagai cara dalam menyusun enam bangun datar (persegi dan atau persegi panjang) yang dapat menghasilkan bangun balok. Adapun beberapa bentuk jaring-jaring balok dapat dilihat pada gambar berikut.

Sumber : http://toriolo.com/jaring-jaring-balok/

Luas Permukaan dan Volume Balok :

Untuk menghitung luas dan volume sebuah balok digunakan rumus berikut.

Luas permukaan balok (Lp) :
\(Lp=2[(p\times l)+(p\times t)+(l\times t)]\)

Volume balok (V)
\(V=p\times l\times t\)

Keterangan :

p : panjang
l : lebar
t : tinggi

Contoh :


1. Perhatikan gambar balok disamping !

    Tentukan :

    (a) Luas permukaan balok
    (b) Volume balok

penyelesaian :
\(p=6\;cm,l=4\;cm,t=3\;cm\)

(a) Luas permukaan (Lp)

\(Lp=2[(p\times l)+(p\times t)+(l\times t)]\)
\(Lp=2[(6\times 4)+(6\times 3)+(4\times 3)]\)
\(Lp=2[(24)+(18)+(12)]\)
\(Lp=2[54]\)
\(Lp=108\;cm^2\)

(b) Volume (V)
\(V=p\times l\times t\)
\(V=6\times 4\times 3\)
\(V=72\;cm^3\)

Pojok Fakta :

Sumber : https://id.pinterest.com/pin/777433954396574244/